Pedras no caminho

Frações e proporção são dois dos grandes gargalos para o aprendizado da matemática, dizem os professores.

Texto: Rubem Barros

Um dos desenhos mais reproduzidos do mundo, fruto de um desafio aceito pelo mestre renascentista Leonardo da Vinci nas últimas décadas do século 15, o Homem Vitruviano sintetiza e expressa as grandes ideias de seu tempo. Num momento de valorização da ciência e do homem, o corpo humano serviu como modelo para que se projetassem os ideais de beleza, harmonia e equilíbrio balanceados pela perfeição de suas proporções. 

A figura, representada em meio a um círculo e um quadrado, tem quatro superposições e seu centro, o umbigo do homem, é o mesmo das duas figuras geométricas. Da Vinci se valeu da proporção áurea, uma constante real, algébrica e irracional que desde os gregos é empregada para a criação de figuras harmônicas e belas, proporções usadas até hoje em muitos artefatos (leia box). 

Esse registro introduz uma reflexão sobre os problemas que seguidamente impedem que a imensa maioria dos estudantes brasileiros se apodere de conhecimentos que lhes permitam “ampliar sua compreensão de si mesmos, do mundo natural e social, das relações dos seres humanos entre si e com a natureza”, como apregoa a BNCC (Base Nacional Comum Curricular).

Afinal, um dos conceitos que não têm sido assimilados por alunos dos Anos Iniciais do Ensino Fundamental é o de proporcionalidade, um tema fundamental que será basilar para o desenvolvimento do pensamento algébrico e da geometria. 

Porém, para chegarmos a caminhos que nos levem a esse conceito, é preciso retroceder. Um dos profissionais que detectaram o problema é o professor Jorge Lira, cientista-chefe do Centro de Excelência em Políticas Educacionais, da Universidade Federal do Ceará (UFCE). “Estamos fazendo um esforço concentrado para fomentar o letramento matemático dos professores, que em grande número apresentam perfil de baixa proficiência matemática”, diz. 

Recorrer a situações do cotidiano que dialoguem, ao mesmo tempo, com o universo dos alunos e com os conceitos matemáticos é uma estratégia enfatizada pela BNCC e corriqueira para muitos professores.

A falta de letramento ou alfabetização matemática resulta em grande parte de cursos de pedagogia com poucos componentes que tratem de matemática ou de seu ensino, carência compartilhada por muitos gestores pedagógicos. Não dominar conceitos básicos da disciplina leva muitos docentes, em especial no Fundamental 1, a atropelar o processo de compreensão dos estudantes.

“No Brasil, em geral, tende-se a ensinar as operações, a soma, a subtração, ou os algoritmos. Eu gosto de fazer oficinas para mostrar como o pensamento algébrico já está sendo construído no primeiro ano. Até os 8 anos, o aluno tem de estar alfabetizado numericamente”, opina Yuriko Baldin, pesquisadora aposentada na área de geometria diferencial e hoje professora do Programa de Pós-Graduação no Ensino de Ciências Exatas na UFScar (Universidade Federal de São Carlos). 

A docente explica que essa alfabetização se dá, como no ensino da linguagem escrita, com a percepção da criança de que o número, assim como o objeto que ela conta, é uma representação da realidade. Essa percepção é importante para que o aluno perceba que a quantidade pode ser a mesma, porém atribuída a objetos diferentes (3 maçãs e 2 bananas). E que o número pode continuar igual, porém com mudança dos elementos representados (1 maçã e 4 bananas). No caso, ambas as situações, 3+2 e 1+4, resultam num total de cinco frutas. O que traz um outro elemento importante para a percepção infantil, a ideia de igualdade. 

“A ferramenta, o instrumento próprio da abstração matemática, chama-se uma coisa simples da nossa vida: igualdade. Quando você percebe que uma coisa é igualzinha a outra, usamos essa palavra. Esse conceito tem de ser definido de forma clara. Maçã não é banana e banana não é maçã, a quantidade é igual, os objetos não”, explica a pesquisadora. 

Óbvia num primeiro momento, a explicação embute o tema da contagem, em que se trabalham habilidades como pareamento, agrupamento, estimativa e comparação de quantidades. “A contagem depois estará ligada ao pensamento algébrico, à transição entre a aritmética e a álgebra”, antecipa Baldin.

Apropriação crescente 

Esse domínio numérico deve ir se sofisticando ao longo dos dois primeiros anos do Fundamental, quando é muito importante o exercício de resolver e formular problemas com adições e subtrações, primeiro com números de dois algarismos, depois também trabalhando com números até 1.000, no 2^o ano, compondo-os e os decompondo. A lida com problemas, seja na sua solução, seja na elaboração, deve estimular o uso de imagens e atividades do cotidiano em que as duas atividades estejam presentes. Esses processos vão se desdobrar em outros anos na modelagem matemática em temas cada vez mais complexos. No campo algébrico, o trabalho com a identificação de padrões de figuras e números e a posterior descrição de regularidades, habilidades previstas na BNCC, também são fundamentais nessa projeção futura. 

Para o trabalho com números de quarta ordem, o milhar, dificuldade que estudantes apresentam com alguma frequência, Ana Elisa Zambon, coordenadora de projetos da Roda Educativa (ex-Cedac), instituição que faz formação de professores em todo o país, busca primeiro identificar o que os alunos já sabem. Essa, aliás, é uma de suas estratégias frequentes de trabalho. 

“Meu grande desafio como professora é identificar o que os alunos já sabem. A base para que eles aprendam matemática é proporcionar problemas a partir do que sabem, do que tenham possibilidade de resolver. Isso independentemente de todos resolverem, pois uma boa situação-problema para um aluno não é para outro, pois trabalhamos com diversidade”, diz Zambon, licenciada em Matemática e ex-professora do Ensino Fundamental na rede municipal de São Paulo. 

Para introduzir o milhar, ela propõe adições a partir de um múltiplo de fácil identificação, por exemplo: 2.000 + 345 (2.000, múltiplo de 10, de 100, de 1.000). As hipóteses do estudante podem levá-lo a começar pela decomposição por múltiplos, valor posicional etc. Trabalhando em grupos, os alunos têm a oportunidade de interagir com outras hipóteses nessa atividade, cujo objetivo de aprendizagem é trabalhar o cálculo e o sistema de numeração (3^o ano). Outro meio de exercitá-los é o ditado dos números, em que ela coloca as respostas na lousa e as analisa, ouvindo as suposições dos estudantes. Assim, antes de chegarem ao ano de 2024, podem passar por 200.024, por exemplo, até o resultado correto.  

Os principais gargalos

É a partir da introdução da operação de dividir e dos números racionais, representados por frações ou por decimais, que as rachaduras do ensino e da aprendizagem se mostram mais nítidas. Com as divisões e a entrada em cena das frações, temos contato com aquele que talvez seja o principal gargalo do ensino da matemática se não nos nove anos do Fundamental, seguramente dos Anos Iniciais. 

Segundo Jorge Lira, entre o 3^o e o 6^o ano, ao lado da utilização das frações, existe também uma primeira aproximação com a modelagem matemática, a formulação em linguagem matemática para dilemas e questões do universo cotidiano, visando à sua resolução. “Nessa fase também se trabalha com a comparação de medidas, com porcentagem, escala, conversão de unidades e proporção”, explica Lira. 

O primeiro entendimento da fração é prejudicado, em muitos casos, pelo fato de os alunos, ao compararem ½ e ⅓, não se darem conta de que o que está posto é a fração, e não os números 3 e 2. Por isso, muitos acreditam que, se 3 é maior do que 2, ⅓ é maior do que ½. “Não veem a fração como uma unidade”, diz Ana Zambon. 

“O grande obstáculo didático é que continua a se introduzir o algoritmo antes que o aluno entenda o sentido de multiplicar ou dividir. O algoritmo é a técnica que ensina a operação, deve ser a fase final da aprendizagem, quando o conceito da operação já está assimilado”, reflete a educadora. 

“Essa ‘valorização procedimental’ – ou talvez pudéssemos chamá-la de obsessão por fórmulas e algoritmos – acaba sendo acentuada pelas avaliações em larga escola, como o Saeb e as provas estaduais”, relata Jorge Lira. “Esses testes são focados quase que exclusivamente no procedimental. Foi feito um paralelo entre essas provas e o Pisa, e a correspondência é com o nível 1 da avaliação internacional. Elas não combinam conhecimentos, não envolvem competências propriamente matemáticas. Esses testes dão um panorama dos sistemas e acabam direcionando os currículos”, conta. 

Talvez esse seja um dos motivos pelos quais é frequente, na comparação de resultados das duas etapas do Ensino Fundamental, sempre se constatar um bom desempenho dos Anos Iniciais em contraste com sérios problemas de aprendizagem nos Anos Finais. A hipótese mais aceita é que as provas dos Anos Iniciais não estejam medindo os conhecimentos mais complexos, que deveriam ser assimilados na etapa. Depois, nos Anos Finais, os resultados apenas estampam as dificuldades que os alunos tiveram já no 6^o ano em campos como álgebra e geometria. Isso sem falar no crônico problema da passagem entre os dois ciclos, quando a mudança abrupta de poucos professores para muitos docentes, cada um com suas exigências, afeta o desempenho de muitos estudantes. 

Auxílio lúdico

Para o trabalho com tópicos tão importantes e delicados da compreensão matemática, a professora Yuriko Baldan recomenda recorrer ao lúdico, como o uso do estojo de frações ou uma fita métrica, material utilizado no Japão, como ela explica. O estojo contém uma base, peças retangulares para encaixe e transparências. Proporciona a percepção da transição entre concreto e abstrato, além de noções de notação, comparação de frações e noções de equivalência. Já a fita métrica é introduzida na educação japonesa no 1^o ano, para que a criança veja que, além do número inteiro, há outras partes que o compõem – e que podem ser restos em determinadas situações. 

Na BNCC brasileira, é recomendado o trabalho com habilidades, por meio de elaboração e resolução de problemas, tanto de multiplicação como de divisão, com os números 2, 3, 4, 5 e 10 na multiplicação, trabalhando estratégias de cálculo. Já as divisões devem ser de um número natural por outro, até 10, com resto zero e maior do que zero. Além disso, associar o quociente de divisões com resto zero de um número natural pelos mesmos 2, 3, 4, 5, 10. Introduz-se assim a ideia de partes de um todo, ½, ¼ etc., trabalhando o significado de metade, ¼ e daí em diante, estabelecendo o conceito de fração. As habilidades recomendadas para os anos seguintes continuarão, tanto no eixo numérico como no algébrico, trabalhando com números racionais e suas variantes (¾, 75%, 0,75).  

Ainda no 4^o ano, a igualdade entra em pauta de novo e, como recomenda a professora Baldin, será resgatada pelo aluno que anos antes havia trabalhado comparativamente as grandezas numéricas. O objetivo aqui é perceber relações como a permanência da igualdade quando dois termos têm subtraído ou adicionado um mesmo número. Ou já descobrir o resultado de incógnitas a partir de outros elementos dados. A álgebra entra em campo e aqui serão necessários os recursos das operações, do uso das frações e da modelagem dos problemas, entre outros. 

Para a professora Ana Zambon, a introdução da linguagem algébrica, das equações, em especial as de 2^o grau, tem como pressuposto o domínio da noção de equivalência. “É isso que permite que o aluno compreenda os mecanismos de jogar para um lado ou para o outro”, diz ela, em relação aos procedimentos de resolução. Ela costuma percorrer esse caminho em três etapas. 

A primeira é o aprendizado da equação de primeiro grau. Num segundo momento, ela trabalha equações com o uso de frações, o que dá a oportunidade de rever tanto o conceito quanto o algoritmo, em especial da divisão de frações. “Por último, sempre dentro de um contexto próximo ao do aluno, proponho o cálculo da área de um determinado espaço. O trabalho conjunto é o segredo da resolução de problemas. Se não sabem a fórmula da área, pensam se há a possibilidade de usar outra estratégia que não a utilize. Nem sempre é possível”, diz, mas o ponto-chave é o exercício do raciocínio e a posterior descoberta da fórmula da área. 

Cotidiano em pauta

Recorrer a situações do cotidiano que dialoguem, ao mesmo tempo, com o universo dos alunos e com os conceitos matemáticos é uma estratégia enfatizada pela BNCC e corriqueira para muitos professores. Norma Dias Carvalho, professora dos Anos Finais do Fundamental e do Ensino Médio na Escola Estadual Luiz Pereira Sobrinho, em Carapicuíba (SP), dá um exemplo de como uma situação, a princípio desconfortável, tornou-se um exemplo concreto enquanto falava sobre proporcionalidade e grandezas. 

Constrangida, uma aluna que havia se atrasado percebeu que, para chegar no horário à escola, teria de aumentar a velocidade na mesma proporção em que o tempo que tinha para o trajeto havia diminuído. “Afinal, a casa dela e a escola estavam no mesmo lugar, o que significava que o espaço a percorrer seria o mesmo. Então, quanto menos tempo, mais velocidade”, recorda a professora. 

Atualmente escrevendo sua dissertação de mestrado em Educação Matemática, Norma Carvalho vem de uma família de professores da área de humanas, mas sempre foi curiosa em relação aos fenômenos físicos. Tem graduação em engenharia eletrônica, depois de fazer o técnico também em eletrônica. 

Em conjunto com seus pares, vem realizando um trabalho de transformação na escola onde atua há 12 anos. Anos atrás, com 98% dos alunos de Anos Finais com conhecimentos abaixo do básico no Ideb, resolveram atuar mexendo com o brio dos estudantes e convencê-los de que não estavam abaixo do nível básico. Separaram os alunos em grupos e ela e outra docente começaram a ministrar aulas aos sábados. Atacaram os principais problemas de aprendizado: divisão, frações e proporção. Com os mais adiantados, aprofundaram o trabalho com álgebra. 

O trabalho com produtos notáveis, expressões algébricas com polinômios, é uma das grandes satisfações da professora, principalmente quando desenvolvidos algebricamente. “Peço que façam demonstrações de problemas, como, por exemplo, inserir dois quadrados perfeitos dentro de um quadrado”, diz. A visualidade ajuda a compreensão do problema. 

“A BNCC é um bom instrumento para trabalhar. É positivo ter um documento norteador, orienta para onde as coisas devem caminhar”, diz a docente mestranda. Ela, porém, é refratária à ideia do uso de plataformas para ensinar. “Você muda de sala e mudam as questões. Não dá para aplicar a mesma fórmula para tudo.” 

As particularidades das escolas públicas exigem sensibilidade para analisar em que contexto os alunos acabam defasados. Sob esse aspecto, o trabalho feito em sua unidade está relacionado a uma das competências específicas da matemática na Base, aquela que recomenda “desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários”.

“As habilidades socioemocionais têm de ser contempladas, trabalhar o aluno como pessoa, para que ele entenda que a matemática é um caminho de leitura do mundo”, diz Norma Carvalho. Hoje, a EE Pereira Sobrinho é a escola de sua região que mais aprova estudantes para as universidades públicas. “No último ano, foram 58 de 200 que prestaram vestibular.”  

Importância para o pensamento

O ensino da geometria como o que Norma Carvalho gosta de realizar muitas vezes é relegado a segundo plano. Segundo Jorge Lira, além de escasso, acaba resumido em um compêndio de fórmulas, sem que haja melhores noções dos conceitos fundamentais da geometria, que, como recomenda a Base, devem ser dados aos estudantes desde o 1^o ano, retomados e aprofundados a cada ano. 

Também nesse campo, as provas de larga escala brasileiras não valorizam um conhecimento em níveis já mais sofisticados. “Os testes são muito focados no pouco que é ensinado, coisas muito preliminares. E a geometria é fundamental para a construção do pensamento lógico-dedutivo e para o raciocínio indutivo, pois possibilita, também, visualizar padrões e fazer inferências”, diz Lira. São recursos do pensamento que a matemática ajuda a construir, mas que são requisitados por várias outras áreas do conhecimento.

O Homem Vitruviano e a Proporção Áurea

Nascido no século 1 a.C., o engenheiro e arquiteto romano Marcus Vitrivius Pollio foi autor de um tratado de arquitetura, o De Architectura Libri Decem. Segundo o Dicionário de Biografias de Pierre Grimal, a obra teve várias edições e suas ideias resgatadas durante a Renascença. “Sua obra não é somente um manual de arquitetura, mas também uma enciclopédia de conhecimentos técnicos e científicos de sua época”, escreve Grimal. 

Para Vitrúvio, o corpo humano era um microcosmo da harmonia universal, análogo ao que era perfeito na natureza, e as edificações deveriam inspirar-se nas suas proporções. Suas ideias foram retomadas em meio à filosofia renascentista, que colocava o homem no centro do universo. Do desenho de Vitrúvio, porém, só havia pistas. 

Leonardo da Vinci utilizou a sobreposição de um quadrado e um círculo, as duas formas então tidas como as mais perfeitas da natureza. Dentro, colocou o homem. A obra faz uso da proporção áurea, ou regra de ouro, descrita pela primeira vez por Euclides, há cerca de 2,3 mil anos, na obra Os Elementos. 

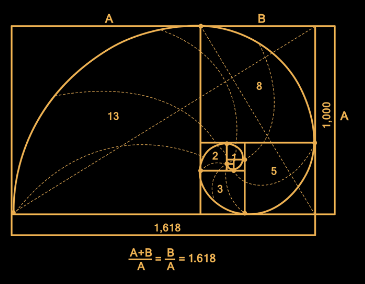
Segundo os tratados matemáticos, é resultado da divisão de uma reta em dois segmentos de tamanhos diferentes. A parte mais longa da reta, quando dividida pela menor parte, deve ter resultado igual a quando se divide a reta completa pela menor parte da divisão. O resultado da divisão tem como valor o número 1,6180339887. Esse número é uma constante real algébrica irracional. 

Edifícios como o Parthenon, objetos como o iPhone, obras de arte e a diagramação de muitos impressos (livros, revistas) são desenhados a partir da regra de ouro.